Understanding the Concept of Fractions: An Introduction for Students

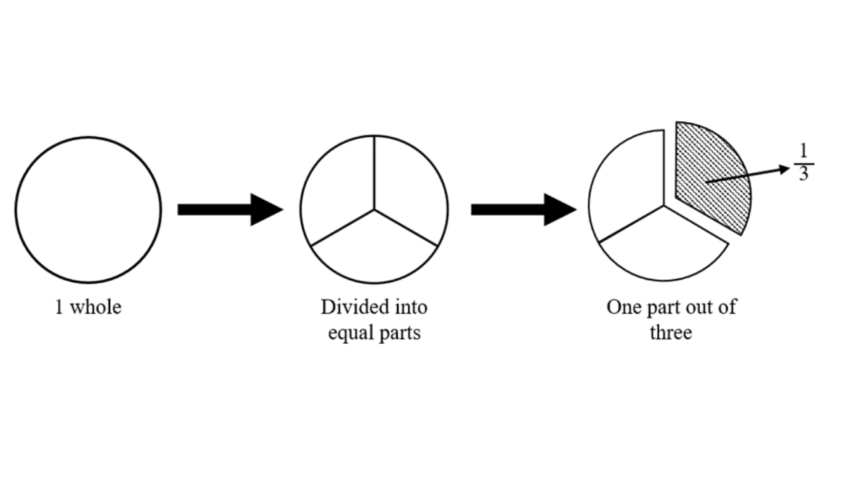
What Are Fractions?

In mathematics, the fraction is a term that is known as the portion of the whole and we say that it represents the whole term in equal parts. As we know the rational term is written as the above and lower value which is separated by the vinculum. The Mixed Numbers to Improper Fractions Calculator is an online tool that provides quick and accurate results for complex fraction operations including their conversion from whole to decimal.

Parts of a Fraction: Numerator and Denominator

• Numerator: The top part of the fraction which is held at the top of the horizontal line is referred to as the fraction. The numerator shows the parts of the number being considered or counted.

• Denominator: The bottom part of the fractional term which is positioned below the horizontal line is known as the denominator. The denominator indicates the number of equal parts that make up the unit.

The concept of these fractional components is manipulated in various mathematical contexts and we say that the combination of both the numerator (Top Value) and the denominator (Bottom Value) fraction is able to be described. This shows the relationship between the part being considered and the whole.

Important Fraction Symbols:

As we know fraction plays a prominent role in many mathematical operations. In order to enhance your understanding we have discussed all these terms in the below section. Free Mixed Numbers to Improper Fractions Calculator also takes into account these symbols to evaluate the solution of given fractional values.

Symbol	Name	Symbol Meaning
+	plus sign	Addition
–	minus sign	Subtraction
*	asterisk	Multiplication
×	times sign	Multiplication
:	division sign	Division
/	division slash	Division
:	colon	Complex fraction
^	caret	Exponentiation/power
()	parentheses	Calculate expression inside the first

Types of Fractions

There are three main types of a fraction are discussed in the below further discussion. The Mixed Numbers to Improper Fractions Calculator offers the calculation for all the fraction types. So you can use it for fraction addition, subtraction, multiplication, and division.

➔ Proper Fraction:

The value in which the numerator is smaller than the denominator is known as the proper fraction. These are always represented as less than the whole unit.

Example: 5/7, 3/8

➔ Improper Fraction:

Improper fraction is the type of fraction in which the numerator is considered greater than the denominator. Improper fractions are easily converted to mixed numbers.

Example: 11/8, 13/5

➔ Mixed Numbers:

As we know the mix means the combination of two or more terms. So here we define the mixed number as the term that consists of whole numbers and the proper fractions.

Example: 2 ¾ , 5 ½

Converting Fractions To Decimals:

With the help of a user-friendly Mixed Numbers to Improper Fractions Calculator you can make your problems easy to input and get instant results. Here we have discussed some methods to change the fractional values into the decimals to enhance and clarify the concept of fractions conversion.

Method # 1 – Simplifying The Fraction

First find the GCF (Greatest Common Factor) of the numerators and the denominators and after that make sure the division process of the numerator and denominator is by the greatest common division.

For Example,

Let’s convert the fraction 20/25 to a decimal using this method.

• Find the GCD of 20 and 25. The GCD is 5
• Divide the numerator & denominator of the fraction by 5. This gives us 4/5
• Convert 3/4 to a decimal by dividing 4 by 5. This gives us 0.8

Method # 2 – Dividing Numerator By Denominator

Same as the above-discussed simplifying fraction method here we also need to divide the numerator by the denominator. The division process keeps going until the numerator is no longer divisible.

For Example,

Suppose a fraction term like 5/9 so solve this one to the decimals.

• Divide 5 by 9. This gives us 0.556.

Method # 3 – Expressing Repeating Decimals As An Infinite Series:

The recurring decimals are the representation that shows the number whose digits are periodic. In this method, we will change the decimal values into the fractional values.

For Example,

Let us consider 1/3 or 5/6.

In this practical supposition, the results are denoted in the form of repeated fractions so this is equals to 0.333… or 0.833…

Table of Conversion Fractions to Decimals

64th	32nd	16th	8th	4th	2nd	Decimal
1/64						0.015625
2/64	1/32					0.03125
3/64						0.046875
4/64	2/32	1/16				0.0625
5/64						0.078125
6/64	3/32					0.09375
7/64						0.109375
8/64	4/32	2/16	1/8			0.125
9/64						0.140625
10/64	5/32					0.15625
11/64						0.171875
12/64	6/32	3/16				0.1875
13/64						0.203125
14/64	7/32					0.21875
15/64						0.234375
16/64	8/32	4/16	2/8	1/4		0.25
17/64						0.265625
18/64	9/32					0.28125
19/64						0.296875
20/64	10/32	5/16				0.3125
21/64						0.328125
22/64	11/32					0.34375
23/64						0.359375
24/64	12/32	6/16	3/8			0.375
25/64						0.390625
26/64	13/32					0.40625
27/64						0.421875
28/64	14/32	7/16				0.4375
29/64						0.453125
30/64	15/32					0.46875
31/64						0.484375
32/64	16/32	8/16	4/8	2/4	1/2	0.5
33/64						0.515625
34/64	17/32					0.53125
35/64						0.546875
36/64	18/32	9/16				0.5625
37/64						0.578125
38/64	19/32					0.59375
39/64						0.609375
40/64	20/32	10/16	5/8			0.625
41/64						0.640625
42/64	21/32					0.65625
43/64						0.671875
44/64	22/32	11/16				0.6875
45/64						0.703125
46/64	23/32					0.71875
47/64						0.734375
48/64	24/32	12/16	6/8	3/4		0.75
49/64						0.765625
50/64	25/32					0.78125
51/64						0.796875
52/64	26/32	13/16				0.8125
53/64						0.828125
54/64	27/32					0.84375
55/64						0.859375
56/64	28/32	14/16	7/8			0.875
57/64						0.890625
58/64	29/32					0.90625
59/64						0.921875
60/64	30/32	15/16				0.9375
61/64						0.953125
62/64	31/32					0.96875
63/64						0.984375
64/64	32/32	16/16	8/8	4/4	2/2	1